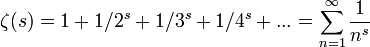Güncel ve Genel Bilgi Desteği
Giriş Sayfanız Yapın Güncel ve Genel Bilgi Desteği Sık Kullanılanlara Ekleyin

Follow @yucinbil
Bernhard Riemann
Yazar admin
Bernhard Riemann
|
Bernhard Riemann, 1863
 |
|
| Doğum | 17 Eylül 1826 Breselenz, Almanya |
|---|---|
| Ölüm | 20 Temmuz 1866 Selasca, İtalya |
| Milliyeti | Alman |
| Branşı | Matematik |
| Çalıştığı yerler | Göttingen Üniversitesi |
| Öğrenim | Göttingen Üniversitesi Berlin Üniversitesi |
| Doktora hocası | Carl Friedrich Gauss |
| Önemli başarıları | Riemann hipotezi Riemann integrali Eliptik geometri |
Georg Friedrich Bernhard Riemann (17 Eylül 1826 – 20 Temmuz 1866), analiz ve diferansiyel geometri dalında çok önemli katkıları olan Alman matematikçidir. Söz konusu katkılar daha sonra izafiyet teorisinin geliştirilmesinde önemli rol oynamıştır. Bu matematikçinin ismi aynı zamanda zeta fonksiyonu, Riemann hipotezi, Riemann manifoldları ve Riemann yüzeyleri ile de bağlantılıdır.
Almanya‘da Dannenberg yakınlarındaki Hanover Krallığının Breselenz kasabasında doğan matematikçinin babası Friedrich Bernhard Riemann idi. Bernhard Riemann altı çocuklu bir ailenin ikinci çocuğuydu.
Riemann, 1840 yılında büyükannesi ile yaşamak ve Lyceum‘u ziyaret etmek için Hanover’e gitti. Büyükannesinin 1842 yılındaki vefatından sonra Lüneburg‘daki Johanneum‘a giden Riemann, 1846‘da yani 19 yaşında Göttingen Üniversitesi‘nde filoloji ve teoloji çalışmaya başladı. En küçük kareler yöntemini anlatan matematikçi Gauss‘un derslerine katıldı. 1847 yılında Riemann’ın babası ona teolojiyi bırakıp matematik çalışması için izin verdi.
1847 yılında Berlin‘e gitti. Burada Jacobi, Dirichlet veya Steiner ders veriyordu. Berlin’de iki yıl kalan matematikçi 1849 yılında Göttingen‘e döndü.
Riemann ilk dersini 1854‘te verdi ve bu dersle sadece Riemann geometrisinin temellerini kurmakla kalmadı aynı zamanda daha sonra Einstein‘in izafiyet teorisinde kullanacağı yapıların da temellerini attı. 1857‘de Götingen Üniversitesi’nde özel profesörlük kademesine terfi etti ve 1859‘da profesör oldu.
1862 yılında Elise Koch ile evlendi.
Selasca, İtalya‘ya doğru gerçekleştirdiği üçüncü seyahatte hayata gözlerini yumdu.
Riemann hipotezi (Riemann zeta hipotezi olarak da bilinmektedir), matematik alanında ilk kez 1859 yılında Bernhard Riemann tarafından ifade edilmiş fakat günümüze kadar çözülememiş problemlerden biridir.
Bazı pozitif tamsayıların kendilerinden küçük ve 1′den büyük tamsayıların çarpımı (örn. 2, 3, 5, 7, …) cinsinden yazılamamak gibi bir özelliği vardır. Bu tür sayılara Asal sayılar denir. Asal sayılar, hem matematik hem de uygulama alanlarında çok önemli rol oynar. Asal sayıların tüm doğal sayılar içinde dağılımı bariz bir örüntüyü takip etmemektedir ancak Alman matematikçi Riemann, asal sayıların sıklığının;
s ≠ 1 olmak koşuluyla tüm s karmaşık sayıları için
biçiminde belirtilen ve Riemann Zeta Fonksiyonu olarak bilinen fonksiyonun davranışına çok bağlı olduğunu gözlemledi. Riemann hipotezinin iddiasına göre
-
- ζ(s) = 0
denkleminin tüm çözümleri karmaşık düzlemde bir doğru üzerinde yer almaktadır. Daha kesin bir söyleyişle, bu denklemin tüm karmaşık sayı çözümlerinin gerçel kısımlarının ½ olduğu tahmin edilmektedir. Bu iddia ilk 1.500.000.000 çözüm için sınanmıştır. Bu iddianın her çözüm için doğru olduğunun ispatlanabilmesi halinde asal sayıların dağılımı ile ilgili çok önemli bilgiler edinmek mümkün olacaktır.
RİEMANN TOPLAMI
Riemann anlamında integralin tanımlanmasında kullanılan toplamdır.

Δxi ler fonksiyonun tanım aralığının sonsuz küçük bölüntüleri, pi ise bu bölüntülerden alınan bir sayıdır. n ise bölüntülerin toplam sayısıdır.
Bu yazı toplamda 6031, bugün ise 4 kez görüntülenmiş
Ev ve İş Telefonu Başvurusu Yapmak İçin; Buraya tıklayınız... Yorum
Yorum
Reklam
Son Eklenenler
- Çiçek Saksıları
- Çocuk Kitapları Web Sitesi Açıldı
- Fabrika İnşaatı Web Sitesi Açıldı.
- Hazır Beton
- Pirelli 2012 Takvimi Çekimi -Galeri
- Kral oyun oyna | Ücretsiz oyun oyna ! hafıza oyunları burada 3
- Oyun Oyna 3d Oyunla Araba Oyunu silah Oyunu flash oyunlar burada
- Fatmagülün Suçu Ne Yeni Sezon İlk Fragmanı sitemizde 2011Fatmagül’ün Suçu Ne Yeni Sezon Fragman Video İzle Kanal D Eylül 2011
- Öyle Bir Geçer zamanki dizisi yeni sezon ilk fragmanı izle
- 2011 Üniversite harçları – üniversite kayıt evrakları 2011-2012
Ayarlar
-
 Ocak 25, 2011
Ocak 25, 2011 -
 Eğitim
Eğitim -
 Yorum yapılmamış
Yorum yapılmamış
-
 RSS Yorumları
RSS Yorumları -
 Del.ico.us
Del.ico.us
-
 Digg!
Digg!